Table of contents
扣细节
-
若题目中给出特定的初始状态,则应考虑在特定的起始状态下的返回值。 例如1646. 获取生成数组中的最大值,应考虑起始状态0和1。
-
在题目最后给出限制条件时,也应考虑在限制条件的边界是否合适,此时往往是最左侧边界。例如274. H 指数,
0 <= citations[i] <= 1000,此时应该考虑citations[i]== 0的情况。
递归
穷尽某种满足条件的各种可能性,可考虑使用递归方法。
- 使用2个function,一个给出原始条件,一个用于递归
- 递归函数直接写在一个function的内部,则有些parameters可以共用。此方法更简约一些
若有附加条件,例如有求得最大值或者最小值,则可以在递归函数中增加限制条件:例如大于某一num的分支不再进行考虑。 由于number 没有reference,可使用list进行保存。例如res=[0]用于保存数量
在递归过程中若使用num来保存数量int类型数据,则在增加时应直接在function中增加,不可在外部例如:
def find(self,num):
self.find(num+1) # 正确
num+= 1
self.find(num) # 错误,因为这很容易导致num混乱,当然若注意到细节处理也不是不可以
Note:提高速度和减少内存的方法,若原有的数组没有二次使用价值,可以在原数组位置上进行修改来减少内存消耗。
动态规划
有时递归方法会超时,此时可以考虑使用动态规划方法。其核心点是要找到当前状态与上一个状态的联系。此时可以考虑使用1维或者2维数组对状态进行保存,同时也应该注意数组初始化时的初始值的设定。
其中的难点就是:
- 如何表述状态和前后两个状态之间的关系。采用的方法可以是用一维或者二维数组先画出简单的例子。
- 找到起始状态,
- 用公式表示前后两个状态的关系。
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
fn_transfer = [[float(inf)]*n for _ in range(k+2)] # 保存的价格为无穷大,表示没有到达此处的航班
fn_transfer[0][src] = 0 # 从出发点的价格为0
# print(fn_transfer)
for i in range(1,k+2):
for j,d,cost in flights:
fn_transfer[i][d] = min(fn_transfer[i][d], fn_transfer[i-1][j]+cost) # 状态转移方程
res = [fn_transfer[t][dst] for t in range(k+2) ] # 求得到达终点的价格
return -1 if min(res) == float(inf) else min(res)
此时column代表的是有多少航班,row代表的是中转次数。数组保存的是价格,
array[0][src]=0表示从出发站价格是0,
Note:{: .label .label-red } 建立二维数组的方法
fn_feature = [[float('inf')*n] for _ in range(k+2)]而不是[[float('inf')*n]]*(k+2)
使用递归方法会超时,这是一个博弈论的问题。
- 状态表述:使用二维数组
dp[i][j]表示在piles 下标为i,j之间时两人手中石子之差。 - 起始状态:当
i>j时dp[i][j] = 0,当i==j时,表示只有一堆石子,dp[i][j]=piles[i]。 - 转移过程:当
i<j时,dp[i][j] = max(piles[i]-dp[i+1][j], piles[j]-pd[i][j-1])。具体的解释可参考官方解释,有动态图方便理解。
下图解释更清楚,具体解释参考 记忆化递归、动态规划(Java) 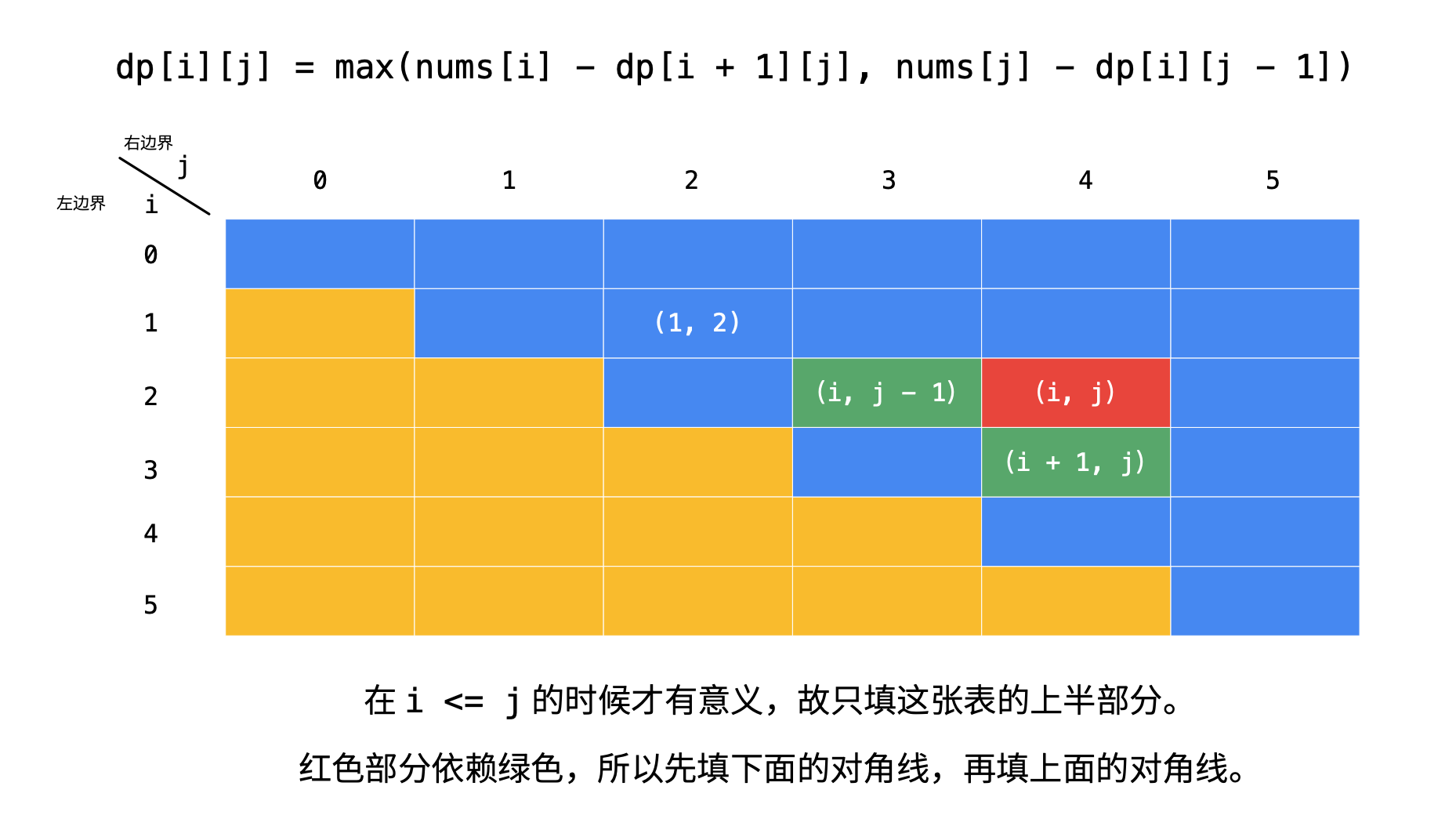
class Solution:
def stoneGame(self, piles: List[int]) -> bool:
# 使用递归超时,尝试使用动态规划(dynamic plane)
n = len(piles)
dp = [[0]*n for _ in range(n)]
for i in range(n):
dp[i][i] = piles[i] # 起始状态
for i in range(n-2,-1,-1):
for j in range(i+1,n):
dp[i][j] = max(piles[i]-dp[i+1][j], piles[j]-dp[i][j-1]) # 转移过程
# print(dp)
return dp[0][n-1] > 0
图的搜索
1. 图的深度搜索 DFS
图的深度搜索就像是走迷宫,需要:
- chalk marks : 作标记,是否来过这一node
- 线团: 可回到出发点,使用recursion来替代作用相当于stack,但是可以对标记进行操作。可以在recursion这一步添加各种条件,比如进入node的数和出node的数。
procedure explore(G , v)
Input: G = (V, E ) is a graph; v ∈ V
Output: visited(u) is set to true for all nodes u reachablefrom v
visited(v) = true # 更改marker
previsit(v) # 可以换成其他的操作
for each edge (v,u) ∈ E:
if not visited(u): explore(u)
postvisit(v)
Note: 以上代码就相当于线团,作用相当于stack
procedure dfs(G)
for all v ∈ V:
visited(v) = false # marker
for all v ∈ V:
if not visited(v): explore(v)
Note: 以上代码相当于marker,一开始把所有的nodes都标记为false,说明没有拜访过。
很多题目可以变相地看作是对图的DFS,例如802. 找到最终的安全状态
2. 图的广度搜素 BFS
使用python 的 deque可实现最短路径的搜索
procedure bfs(G , s)
Input: Graph G = (V, E ), directed or undirected; vertex s ∈ V
Output:For all vertices u reachable from s, dist(u) is set to the distance from s to u.
for all u ∈ V: # marker : 标记没有拜访过
dist(u) = ∞
dist(s) = 0 # 起始点距离设为0
Q = [s] (queue containing just s)
# 以下就是 queue的功能了,first in first out
while Q is not empty:
u =eject(Q)
for all edges (u,v) ∈ E:
if dist(v) = ∞:
inject(Q, v)
dist(v) = dist(u) + 1
Note: 在python中可以使用deque行使queue函数的功能,且deque的功能更强大,查看python 知识点 deque
815. 公交路线。这道题是图的广度算法的演化,更有深度,其表现是把整个公交车作为图中的一点,而使用set这一数据结构来进行剪枝。并且在while循环中使用两个for loop来对每辆公交车每个站点的全部扫描,图解释如下:
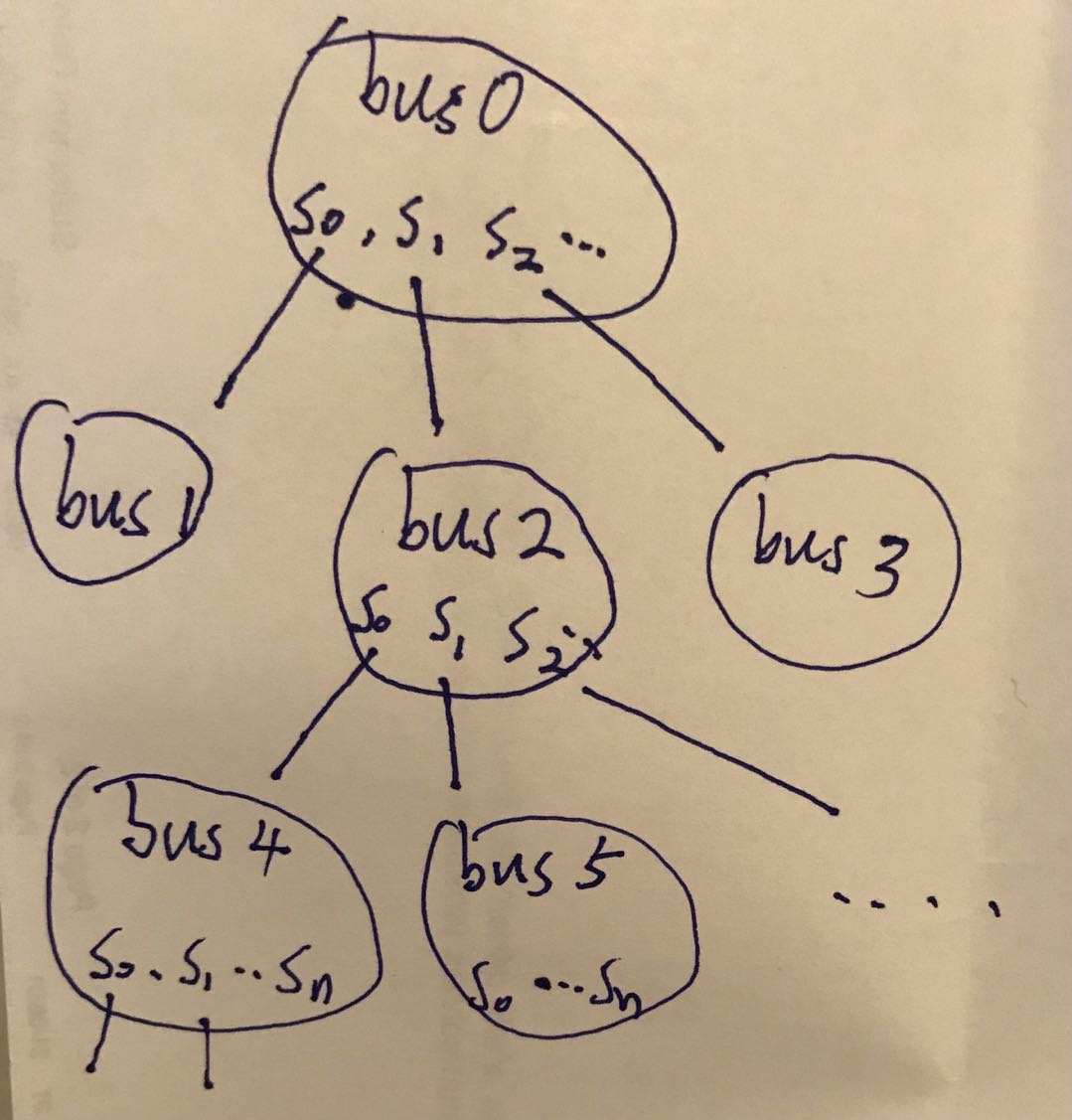
Note:图中每个bus就相当于一个节点,每个节点往外延伸的方向由每个bus的站点(station)决定,之所以需要两个for loop 则是要遍历每层bus和每个bus中的stations。详细的python解释和解题方法参考Benhao
图的广度搜索之Dijkstra 算法
若图中点与点之间的距离是不同的,因此上一个广度搜索算法则不合适。Dijkstra的方法是相当于设定了一个闹钟,用一个数组保存到达一点所需的时间。开始时此数组(list)都是∞(float(‘inf’)),list[s]=0,把起始点的距离设为0。然后使用堆来提取当前距离最短的点,在python中可以使用heapq来保存(t,v): t 在这里可以理解为距离,v理解为图中的vertex。算法如下:
Dijkstra’s shortest-path algorithm.
--------
procedure dijkstra(G,l,s)
Input: Graph G = (V, E ), directed or undirected; positive edge lengths {le : e ∈ E }; vertex s ∈ V
Output: For all vertices u reachable from s, dist(u) is set to the distance from s to u.
for all u ∈ V:
dist(u) = ∞ # 相当于设定了闹钟
prev(u) = nil # 可以用于保存上一个节点
dist(s) = 0 # 起始点的时间设为0
H = makequeue (V ) (using dist-values as keys) # 建立堆
while H is not empty:
u = deletemin( H ) # 提取出现在为止用时最少的vertex
for all edges (u,v) ∈ E:
if dist(v) > dist(u) + l(u, v): # 比较运行时间,选择用时最少的。l(u,v) 为从u到达v点的用时或者距离
dist(v) = dist(u) + l(u, v)
prev(v) = u
decreasekey(H, v) # 把v放到堆中,
Note:
if dist(v) > dist(u) + l(u, v)比较dist[v] 与dist[u]+l(u,v)的距离,即是原本的dist[v]少还是从u到v花的时间少。
- 如果原本的时间少,说明之前已经拜访过了,因为是保存第一次到访的时间,如果没有到访过,应该是∞。
- 如果是从u到v花的时间少,则说明v还没有拜访过,则把
(dist(v), v)放到heapq中。
heapq 的知识见python知识点
例题详见743. 网络延迟时间
N叉树的遍历
本文内容摘自N叉树基础(含四种遍历,图文详解)。
先以二叉树的遍历为例进行说明:
- 前序遍历: 首先访问根节点, 然后遍历左子树,最后遍历右子树。
- 中序遍历: 首先遍历左子树, 然后访问根节点,最后遍历右子树。
- 后序遍历: 首先遍历左子树, 然后遍历右子树,最后访问根节点。
- 层序遍历: 按照从左到右的顺序,逐层遍历各个节点。
Note:从上面可以看出前3种方式主要是根据根节点的位置来进行划分。这3种方式是通过递归来完成。而层序遍历则是要把N叉树转化为图,然后使用图的广度搜索进行遍历。
二叉搜索树
二叉搜索树具有如下性质:
- 结点的左子树只包含小于当前结点的数。
- 结点的右子树只包含大于当前结点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
因此使用中序遍历则可以生成递增序列。例如230. 二叉搜索树中第K小的元素
二叉树的搜索一般有两种方法:
- 递归
- 迭代
迭代方法只是把递归中的stack函数显式地表达出来。
# 递归
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
ans = []
def dfs(node):
if node != None:
dfs(node.left)
ans.append(node.val)
dfs(node.right)
return
dfs(root)
return ans[k-1]
# 迭代
class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
ans = []
stack = [] # 保存left nodes节点
while root != None or len(stack) != 0:
while root != None:
stack.append(root)
root = root.left
root = stack.pop()
ans.append(root.val)
root = root.right
if len(ans) == k: # 增加判断标准
return ans[-1]
转化为图进行操作
因为在题目中二叉树只是向下进行搜索,而距离为K的节点也有可能在上面的父节点,因此简单的二叉树搜索并不合适。一开始想使用(row,col)来表示节点的位置,left node is (row+1,col-1), right node is (row+1,col+1). 但是这里遇到的问题是两个子树中可能会出现相同的(row,col)。如果仅仅是求从root节点距离为K的节点,则直接统计row==k 的节点的值就可以。但是,本题target并不一定是root。
宫水三叶的观点不错,首先把二叉树看作是一个无向图。然后把二叉树转化成图,然后使用BFS(广度搜索)进行扫描距离target为k的点即为要寻找的点。
因为不能保证二叉树中的节点是从0~n-1,本题中我使用defaultdict来储存图graph = defaultdict(list)。所以使用dictionary节省内存。先使用dfs生成无向图,然后使用bfs生成从target到达各点的距离。即可获得结果。
在这里需要注意的是,在bfs中同样适用defaultdict来储存从target到达节点的距离。而起始距离为float('inf'),因此需要这样使用defaultdict:dist = defaultdict(lambda : float('inf'))
在这里有一个python的知识点:defaultdict的使用
from collections import defaultdict
dic_count = defaultdict(int) # 用于计数, default value is 0
dic_list = defaultdict(list) # 用于储存数组, default value is [],a empty list
dic_labmda = defaultdict(lambda : 'ok')
# default value is the return value in the lambda, here is 'ok',
# you can also set other values such as empty string, float('inf')
基本思路是使用dfs 对树中的每个节点设定(row,col),然后进行排序即可。
从相邻的元素求得完整的数组:先通过defaultdict构造成graph,思路一是通过BFS遍历,看能否找到最后的距离为n-1的数组,发现这个容易超时,这是由于起始点没有选好的缘故,可以通过对defaultdict中的value进行排序,然后选择value只有1的key,以此为起始点,应该也可以。 在构建完整数组时,如何查看新加入的数组是不存在愿数组的,一开始可能考虑到的是通过val not in list,但是这样很费时。其实可以使用visited = defaultdict(lambda :False)来查看是否存点已拜访过了。这样就大大节省了时间了。因此要学会灵活运用python自带的数据结构。
就像是走华容道的游戏,其是一个2x3的矩阵。为了计算方面我们可以把2x3的矩阵转化成一维矩阵。如何转化为图的算法呢。首先每个node是board 的状态,如果这个状态是我们所需要的则返回距离,如果不是则继续进行搜索。这样的图与我们之前看到的不同,它是不断生长的,一开始我们并不知道所有的nodes.它是在进行中不断产生新的nodes。
import copy
class Solution:
def slidingPuzzle(self, board: List[List[int]]) -> int:
board_arrange = board[0] + board[1] # 转化成为一维数组
board_right = [1,2,3,4,5,0]
start = (board_arrange, 0 )
seens = []
ans = []
self.bfs(start, board_right, seens,ans)
if len(ans) == 0:
return -1
else:
return min(ans)
def bfs(self, start, board_right, seens,ans):
# print(start)
q = deque([start])
while q:
# print(q)
(board,dist) = q.popleft()
if board == board_right:
ans.append(dist)
return
if board not in seens:
seens.append(board)
else:
continue
index = board.index(0)
row,col = self.index2rc(index)
# 每个node都可能产生潜在的4个新的nodes
for r,c in [(row+1,col),(row-1,col), (row,col+1), (row,col-1)]:
if 0<= r<= 1 and 0<= c <= 2: # 对图进行剪枝
nindex = self.rc2index(r,c)
nboard = copy.deepcopy(board) # 必须使用copy,因为list 是reference。
nboard[index] = nboard[nindex]
nboard[nindex] = 0
q.append((nboard,dist+1))
def index2rc(self, index): # index 转化成row 和 col,方便在board中进行移动
row = index // 3
col = index % 3
return row,col
def rc2index(self,row,col): # row 和 col 转化成1维的index,方便修改一维数组
return row*3 + col
此题也可转化成对图的广度搜索,思路如上面的题类似。一开始我的思路是正确的:像这种寻找最少的操作步数等问题可以转化为对图的广度搜索。而图中的每个节点就是此时操作的状态。在本题中,为了减少操作,我使用seens = defaultdict(lambda : False)来保存每个状态是否出现过。在deadends中的状态都为True。具体解题思路可看我自己的解题方法。
双向BFS可以大大地缩减搜索时间,值得考虑
最长上升子序列
根据题意可知有两个整数数组:target 和 arr,如何通过在arr添加整数使其包含target这个子序列。开始时是想通过动态规划算法,问题在于这种方法会超时。基本思路为:n=len(target), m = len(arr). matrix = [[0]* n for _ in range(m) ] matrix[i][j] 是 arr[0:i+1] 与 target[0:j+1] 之间相同的子序列。 以下解法来源于[Python/Java] 最长上升子序列
class Solution:
def minOperations(self, target: List[int], arr: List[int]) -> int:
# 分析:
# 本题要找最少操作次数,实际上就是找最长的公共子序列(这样需要的操作最少)
# 根据target中互不相同,我们知道每个数字对应的坐标唯一
# 于是最长公共子序列等价于arr用target的坐标转换后构成最长的上升子序列
# 数字对应坐标
idx_dict = {num: i for i, num in enumerate(target)}
# 300.最长上升子序列
stack = []
for num in arr:
# 只有在target的数字才可能属于公共子序列
if num in idx_dict:
# 转换坐标
idx = idx_dict[num]
# 该坐标在当前栈中的位置
i = bisect.bisect_left(stack, idx)
# 如果在最后要加入元素,否则要修改该位置的元素
# 跟一般的讲,i代表了目前这个idx在stack中的大小位置,
# 在前面出现还比idx大的stack中的元素是无法和idx构成最长上升子序列的。
# i左边的数比idx小,可以和idx构成上升子序列,(idx构成的长度就是i+1)
# idx比i的值小,将i替换后可以方便后面构成更优的子序列(越小后面能加入的数越多)
if i == len(stack):
stack.append(0)
stack[i] = idx
# 最终stack的长度就构成了最长上升子序列的长度,用减法即可得到本题答案
return len(target) - len(stack)
# 作者:himymBen
# 链接:https://leetcode-cn.com/problems/minimum-operations-to-make-a-subsequence/solution/python-zui-chang-gong-gong-zi-xu-lie-by-r3yje/
# 来源:力扣(LeetCode)
# 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这道题是直接在数组中寻找严格递增的最长子序列,并没有再进行二次利用。在官方解题方法中有2种方法,分别是动态规划和 贪心+二分查找
# 动态规划
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
dp = [0]*n # dp[i] 保存以nums[i]结尾的的递增最长子序列的长度
if n == 1:
return 1
for i,e in enumerate(nums):
dp[i] = 1 # dp[i]的起始状态
for j in range(i):
if e > nums[j]:
dp[i] = max(dp[i],dp[j]+1) #状态转移过程
# print(dp)
return max(dp)
Note:使用动态规划的核心思想就是如何进行状态转移:dp[j] 表示以nums[j]结尾的最长递增子序列的长度,如果后面的数大于nums[j],则可以加到dp[j]的后面使其长度加1,因此,
dp[i] = max(dp[i],dp[j]+1),最后求dp数组的最大值。
这道题目仅仅是求最长递增子序列的长度,并不要求其具体的排列顺序,因此可以通过贪心+二分法求解。
# 贪心+二分法
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
ls = []
for v in nums:
if ls == []:
ls .append(v)
elif ls[-1] < v: # 大于ls最后一个数就加到ls末尾
ls.append(v)
else:
i = bisect.bisect_left(ls,v) # 目的是让ls的增幅近可能的小,因此代替ls中增幅大的值,
#虽然有可能破坏ls中数刀顺序,但是并不影响长度,因此此方法是可行的
ls[i] = v
# print(ls)
return len(ls)
Note:
i = bisect.bisect_left(stack, idx)这一个是重点 这里有一个python的知识点bisect.bisect_left(stack,idx):通过2分法排序查找idx 在stack中位置(从左边开始),若bisect.bisect_right(stack,idx)则是从右边开始数。详见python知识点
此题与上一题非常接近,同样也可以使用动态规划进行求解,只是需要再加一个数组计算dp[i]这一长度的数目,并在统计过程中对最长数目进行统计。
class Solution:
def findNumberOfLIS(self, nums: List[int]) -> int:
n, ans,maxlen = len(nums), 0, 0
dp = [0]*n # 保存以nums[j] 结尾的LIS长度
cnt = [0]*n # 保存以nums[j] 结尾的LIS长度的数目
for i, e in enumerate(nums):
dp[i] = 1
cnt[i] = 1 # 起始状态
for j in range(i):
if e > nums[j]:
if dp[j] + 1 > dp[i]: # 与求最长LIS问题方法一致
dp[i] = dp[j] + 1 # 重置
cnt[i] = cnt[j]
elif dp[j] + 1 == dp[i]: # 需注意这一步,
cnt[i] += cnt[j] # 增加量
if dp[i] > maxlen:
maxlen = dp[i] # 重置
ans = cnt[i]
elif dp[i] == maxlen: # 增加量
ans += cnt[i]
return ans # 直接出结果
最长公共子序列
求两个字符串的最长公共子序列,可以使用动态规划。其关键点是需要增加一列边界,目的为 当两者之一为空时,最长公共子序列为0. 然后使用两个for loop 来比较两个字符串的每个 字符的匹配情况。其详细的解说可参考原题解说
这道题其本质与上一题相同,就是求得最长公共子序列后,再使用两个数组的长度剪去最长公共子序列的长度即可。
双指针
双指针的作用:slow, fast OR (left,right)
- 若slow,fast在一个series 上进行移动,且移动的距离相同,则可以对固定间隔的数据进行处理
- 同样是在一个series上进行移动,若两者移动的速度不同,则可以用于求环。例如LeetCode 457. 环形数组是否存在循环, slow 每次移动一步,fast每次移动两步,然后通过比较
slow == fast来判断是否存在循环。 - 若slow,fast 在不同的series上进行移动,则可以对两个series上的数据进行比较。例如Leetcode524. 通过删除字母匹配到字典里最长单词,通过两个指针来判断两个字符串是否可以通过删除使其两者相同。
链表
在处理链表问题时一般有两个大方向:
- 先把链表中的数据提取出来,然后根据这些数据重新建立链表
- 根据要求更改链表node 之间的链接
例如430. 扁平化多级双向链表,官方给出的解题思路是第二种,要求思维清晰。我对其不慎了解。需进一步加强。
- 在处理链表问题时,如果需要对多个node进行处理,则可以使用dictionary保存node的节点,这样就很容易的找到想要的节点。
- 分割链表时,应保存两个node:一个是当前的node(head),一个是上一个node(pre),即上一个链表结束的node,开始时两个是同一个node。这样分割时只要使
prev.next=None就可以得到分割链表。例如725. 分隔链表
转化成几何问题
在数组上操作,求其面积相关或者可以转化成与面积相关的问题可以先转化成几何问题,此问题一般可以使用双指针进行解决。例如Leetcode 1838. 最高频元素的频数
一开始我想使用等差方法从最右端开始逐一验证此位点是否是为频数数值。这种方法会超时。
通过看解题方法,发现可以转化成几何求面积问题,使用双指针(left,right)进行滑动窗口,窗口距离只能大不能减小。答案可见链接。其解决的问题主要是right 向右一直增加,一旦k值不足以填补缺口面积则left指针向右加1,这样相当于整体向右移动一步,此时k值应该加上之前补加的面积(看链接的图更明显)。
如果问题是关于有序的数组,只是关心其中的一部分,并有一定的限制条件,可以考虑使用双指针来提高效率。分以下情况:
- 开始时left,right指针从同一方向出发,right 比 left 多1步。两指针根据条件分别移动。
- 开始时left在最左侧,right在数组的最右侧,然后两者分别向中间靠拢。两指针根据条件分别移动
前缀和
560. 和为 K 的子数组 前缀和就是在数组中前n个数的和。我们可以使用一个数组来保存前缀和
# nums : 数组
# prefix : 保存前缀和
n = len(nums)
prefix = [0]*(n+1)
prefix[0] = 0 # 这步要牢记,没有元素时和是0
for i in range(n):
prefix[i+1] = prefix[i] + nums[i]
在leetcode 560 中,想要求得子数组和为k的个数,可以通过统计prefix[i]-prefix[j] == k 的个数来获得。前提是这需要使用2个for 循环,在本题下会超时,所以还需要进行优化。改变方程式为prefix[i] - k == prefix[j],这时我们需要统计在以i为节点的前缀和中之前的前缀和是否有等于prefix[i] - k 的个数。因此我们可以使用defaultdict来统计,快速高效。
Note:{: .lable}
accumulate([1,2,3,4,5,])-> [1,3,6,10,15]可直接生成前缀和
def subarraySum(self, nums: List[int], k: int) -> int:
n = len(nums)
# 求前缀和
prefix_sum = [0]*(n+1)
for i in range(n):
prefix_sum[i+1] = prefix_sum[i] + nums[i]
# 使用defaultdict保存在i之前前缀和的统计个数,
dic = defaultdict(int)
dic[0] = 1 # 目的为保证数组的单个元素满足条件 nums[i] == k
cnt = 0
for i in range(1,n+1): # 以i结尾的数组
left = prefix_sum[i] - k
cnt += dic[left]
dic[prefix_sum[i]] += 1 # 把prefix_sum[i] 保存到prefix_sum 中
return cnt
剑指 Offer 42. 连续子数组的最大和, 其思路为前缀和的最大值减去前缀和的最小值就是到现在为止的最大的子数组最大的和。
930. 和相同的二元子数组: 一开始本想着使用前缀和,先求出前缀和再使用defaultdict统计在前缀和中各数出现的频次,由于原数组nums只有0 和 1, 因此前最和是递增序列,然后计算prv[i]-goal在defaultdict出现的频次。但是这种方法,并不适合当goal=0的情况。因此还要单独对此情况进行处理。因此消耗时间较长,方法如下:
class Solution:
def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
# 求某一个区间的和,因此可以考虑使用前缀和
if goal == 0: # 先求goal = 0的情况
ans = 0
cnt = 0
for i in nums:
if i == 0:
cnt += 1
ans += cnt
else:
cnt = 0
return ans
n = len(nums)
pre = [0]*(n+1)
for i,e in enumerate(nums): # 求前缀和
pre[i+1] = pre[i] + nums[i]
# pre = pre[1:]
dic = defaultdict(int) # 统记前缀和各数出现的频次
for e in pre:
dic[e] += 1
cnt = 0
for i in range(n+1):
res = pre[i] - goal # 统计 pre[i] - goal 在dic 中出现的频次
cnt += dic[res]
return cnt
Note:先求出前最和再使用
res = pre[i] - goal,这种方法适合递增序列。如果不是递增序列,则会统计后面出现的数。因此会失败。下面一种方法把求前最和的思路和统计res = pre[i] - goal的思路放到了一次,且pre[i] - goal为只是在i之前出现的前缀和
class Solution:
def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
# 求某一个区间的和,因此可以考虑使用前缀和
dic = defaultdict(int)
cnt = 0
sum_ = 0
dic[0] = 1 # 这一步很重要
for i in nums:
sum_ += i # 前缀和
cnt += dic[sum_ - goal] # 求pre[i] - goal 在dic中出现的频次
dic[sum_] += 1 # 添加前缀和到dic中
# cnt += dic[sum_ - goal]
return cnt
Note:
dic[0]=1这一步很关键,同时为了保证所求的pre[i] - goal在dic中出现的频次,应该把cnt += dic[sum_ - goal]放在dic[sum_] += 1之前,说明是求i之前的前缀和。
由以上解题方法可以总结出两个数直接的关系操作,例如求两个数的和,两个数的差等等,为了不使用两个for 训练,可以使用哈希函数来保存每个数的个数,然后使用差值在哈希表中寻找另一个数。 前提是把nums排序,然后使用一个for 循环即可。例如题1711. 大餐计数,就是通过这种方法仅使用一个for循环即可。
此题的背景是二叉树,我们知道在求连续的子序列的和时可以使用前缀和,并且为了追求时效,我们还可以使用defaultdict保存前缀和出现的频次,然后使用ans += dic[val-sum]在一个for loop中即可求得结果。
此题的特别之处在于如何在二叉树背景下使用前缀和。一开始我的思路是先求得每个node的前缀和,然后使用list保存(node,pre),即每个node的preference和parent value。然后再进行一遍搜索,这样的话会非常耗时。这种方法可以解出来,解题方法参考第一版解题思路.
改良的方法只需要遍历一次就可以。算法如下
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
# 前缀和, 使用defaultdict 保存val-targetSum的数目
dic = defaultdict(int)
dic[0] = 1 # 这一步很重要
ans = [0] # 用于保存结果
def bfs(node, pre, ans):
if node != None:
pre += node.val
ans[0] += dic[pre-targetSum] # 这一步节省时间
dic[pre] += 1
bfs(node.left, pre,ans)
bfs(node.right, pre, ans)
dic[pre] -= 1 # 这一步很重要,只分析一个侧枝,不影响其他旁支
else:
return
bfs(root, 0, ans)
return ans[0]
差分
-
对于原始数组arr[a, b, c, d],其差分数组为:diff[a, b-a, c-b, d-c]
-
差分数组的前缀和数组 == 原始数组,即:求差分数组的前缀和数组,即可还原回去。[a, a + b-a, a+b-a + c-b, …]
-
对原始数组的区间增加,可以转化为对其差分数组的两点增加( O(n) -> O(1) ): 假设对arr[i … j]区间每个元素全部增加delta,则等价于:diff[i] += delta,diff[j+1] -= delta
本题的关键点是如何做到对数组的区间数据都加一个数。
线段树与完全二叉树
二叉树的相关知识可查看简书,利用数组可以储存二叉树结构,如果是完全二叉树则可以充分利用数组的内存来进行储存,不必像链表一样再设立指针来指向一个节点,节约内存。
数组来储存二叉树根节点(root)的index=1,第0位置可以空着。若父节点为i,则左节点为2*i, 右节点为2*i+1。如下面例子中所示 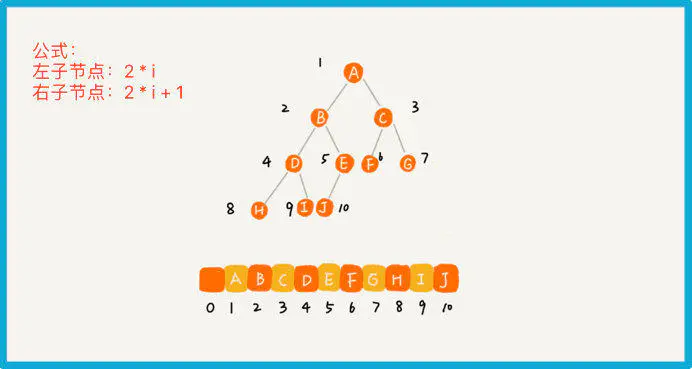
线段树,我的理解是使用数组结构形成的完全二叉树来对某一数据进行检索,修改。为什么使用线段树呢?因为线段树可以把检索时间减少到O(logn)。例如leetcode 307. 区域和检索 - 数组可修改,此题很好的阐释了线段树的作用和优势。
class NumArray:
def __init__(self, nums: List[int]):
self.nums = nums
self.n = len(self.nums)
self.tree = [0]*2*self.n
#创建完全二叉树,先把叶子节点填补上
i,j = self.n,0
while i < 2*self.n:
self.tree[i] = self.nums[j]
i += 1
j += 1
# 从n-1 节点开始倒退计算中间节点,tree[i] = tree[2*i] + tree[2*i+1] 计算而来,root 在数组的index=1
i = self.n-1
while i > 0:
self.tree[i] = self.tree[2*i] + self.tree[2*i+1]
i -= 1
def update(self, index: int, val: int) -> None:
diff = self.tree[index+self.n] -val
self.tree[index+self.n] = val
# 由于只是改变了二叉树中的一个叶子节点,因此只需要改变这个节点和与之相关的父节点即可,父节点可通过diff改变
p = (index + self.n ) // 2
while p > 0 :
self.tree[p] -= diff
p = p // 2
def sumRange(self, left: int, right: int) -> int:
l = left + self.n # 到达在tree中的叶子节点
r = right + self.n
sum_ = 0
while l <= r:
# 如果左边界的index不是偶数,说明是在二叉树节点的右节点,这是我们不能利用其父节点的和相加
# 因此我们需要直接把此叶子节点加到sum上,然后把左边界向右移一个节点到达可以使用父节点求和的
#叶子节点,在下面的 l = l // 2 就是到达了父节点
# 且在二叉树中左节点的index都是偶数2*i, 右节点都是奇数 2*i+1;
# 因此把左边界在右节点的情况下对节点直接相加,然后移动节点到达下一个左节点
#
if l %2 == 1:
sum_ += self.tree[l]
l += 1 # 到达完整的叶子节点的左边界
if r % 2 == 0:
sum_ += self.tree[r]
r -= 1 # 到达完整叶子节点的右边界
l = l // 2 # 到达父节点
r = r // 2
return sum_
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)
例如存在数组nums = [2,4,5,7,8,9],可以把数组转化成下面的二叉树。格式为index/value,其中数组中的数都在叶子节点。对sumRangefunction解释一下:若left=8, right=9,则在最后会达到index=2 value = 29,此时index都为2,因此总有if中对sum_要进行增加。 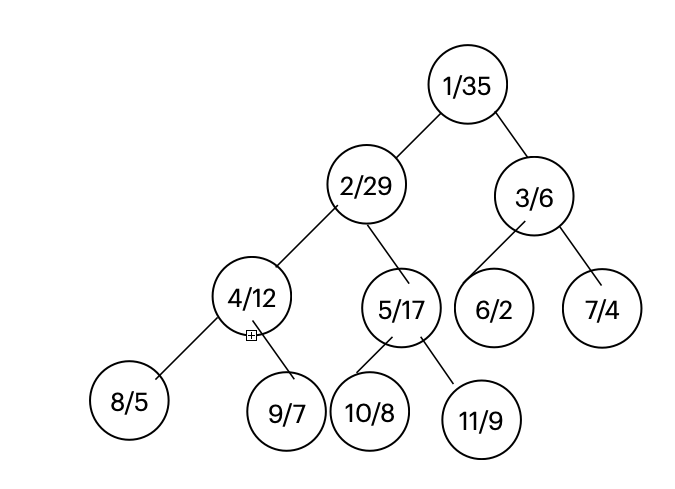
前缀树(Trie)
Trie 树(又叫「前缀树」或「字典树」)是一种用于快速查询「某个字符串/字符前缀」是否存在的数据结构。 其核心是使用「边」来代表有无字符,使用「点」来记录是否为「单词结尾」以及「其后续字符串的字符是什么」 如下图所示: 
建立Trie树的关键是使用一个Node来表示下一个字符,我习惯使用defaultdict,以防止出现KeyError。 例如208. 实现 Trie (前缀树)。 以下代码只截取了初始化函数和insert函数。
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.children = defaultdict(Trie)
self.is_word = False # 判断到这个节点是否是单词
self.flag = False # 判断此节点是否有children
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
nxt = self
for ch in word: # 一个字符一个字符的插入,如果此word与前缀相同则会按照前缀的路线进行直到不同的地方
nxt = nxt.children[ch]
nxt.flag = True # 当前node有children
nxt.is_word = True
另一个leetcode 题目是 212. 单词搜索 II, 在网格中搜索单词。
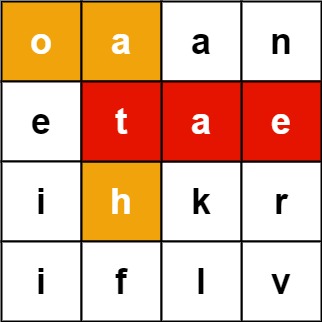
一开始我尝试使用递归方法,但是在倒数第2个测试时超时。因此这种题使用递归是可行的,不过不够有效率。使用Trie Tree可以解决这一问题,思路是先建立前缀树,然后在网格中逐一以网格中的字符开始查看是否可以从前缀树开头查找到单词,在这一步中同样也会用到递归,但是潜在的候选单词明显减少,因为一旦前缀不合适,也不会再检查后面的单词了。
Note: 在对 m x n 二维字符网格 board进行操作时,若题中有限制不能重复利用已经使用的字符则可以通过以下代码来规避。
ch = board[row][col]
board[row][col] = '#' # board中不存在的字符
# code: operatation on the board
board[row][col] = ch
区间修改+单点查询
可对此问题进行总结,并做相关的问题。
对Matrix 进行操作
给你一个matrix,对 行/列/3x3小matrix进行查询或操作.
- 提取row 很简单,一个for循环即可
- 提取column 可先转化成长字符串然后使用截取方法
- 提取3x3 方格数据: 可先通过行分别截取,然后再整合在一起,这样在新的字符串中每9个字符既是3x3方格数据
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
# 先转化成长字符串,然后再分别判断行,列,3x3 宫内是否合规
# check rows
for r in board:
if not self.check(r):
return False
long_str = [''.join(x) for x in board]
long_str = ''.join(long_str)
n = len(board)
# check columns
for i in range(n):
col = [long_str[i+n*r] for r in range(n) ]
if not self.check(col):
return False
# check 3x3
smatrix = []
sm1,sm2,sm3 = [],[],[]
for r in board:
sm1 += r[:3]
sm2 += r[3:6]
sm3 += r[6:]
smatrix += sm1 + sm2 + sm3
for i in range(n):
sm = smatrix[i*n:(i+1)*n]
if not self.check(sm):
return False
return True
def check(self,s)->bool:
form_s = [x for x in s if x != '.']
dic = collections.Counter(form_s)
if sum(dic.values()) == len(dic):
return True
else:
return False
配对
一般是通过stack进行配对,若其中的字符有多种配对的可能性,则需要多于一个的stack来保存不同的字符,配对时需要考虑字符的位置, 则在stack中直接储存字符的index,然后决定stack的不同配对顺序。最后跟据stack剩余的数量决定是否可以完全配对。例如 有效的字符串 Leetcode-678
如果字符串里面仅仅是存在‘(’ 或者‘)’ 则可以使用一个stack解决,但是”*” 可以是’(‘,’)’ or empty string。因此一个stack就不够用了。
一开始使用stack + 递归方法进行暴力解决,但是很容易超时,显然一个* 就有3种可能性,相当于一个for loop。
官方给出的解题思路中:使用2个stack来进行解决。 一个leftstack 保存 ‘(‘ 的位置, starstack 保存 *在string 中的位置,若出现‘)’先使用leftstack 进行匹配。需注意的是在对leftstack and starstack 进行配对时,the index in leftstack must be larger than the index in starstack.
关注整体
有的题目需要关注整体,而忽略具体的细节。例如517. 超级洗衣机 , 开始没有弄明白,想使用图算法解决,但是在方向移动上不知如何进行。具体的解释可参考官方解题
逆向思考
有时根据题意的方向思考很难有清晰的思路。可以尝试反向思考。例如453. 最小操作次数使数组元素相等。根据题意每次操作将会使 n - 1 个元素增加 1。其反向思考是相当于只有一个元素减1。这样考虑题目马上变得简单。
数据结构
有待深入理解python Iterator
拆分submodule
有的题可以把整体拆分成submodule,然后把难度也进行降低。例如95. 不同的二叉搜索树 II
“二叉搜索树关键的性质是根节点的值大于左子树所有节点的值,小于右子树所有节点的值,且左子树和右子树也同样为二叉搜索树。” from 官方解释
因此我们的解题思路是分别生成左子树和右子树然后再进行拼接,形成完整的二叉搜索树。代码如下:
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
def dfs(start,end):
if start > end :
return [None,] # 关于这一点还没有弄明白
allTrees = []
for i in range(start,end+1):
leftTrees = dfs(start,i-1)
rightTrees = dfs(i+1,end)
# 拼接树
for l in leftTrees:
for r in rightTrees:
head = TreeNode(i)
head.left = l
head.right = r
allTrees.append(head)
return allTrees
return dfs(1,n) if n else []
quickSort
def quicksort(array,left,right):
"""Quick sort the array in acending order recursivley
Parameters
---------
array : list
A list of numbers
left : int
The index of array
right : int
The index of array
Return
---------
sorted array in acending order
"""
# 先写明结束条件
if len(array) == 1:
return array
if left >= right:
return array
else:
part_index = partition(array,left,right) # 重新排序subarray,并返回分割index
quicksort(array,left,part_index-1) # 递归
quicksort(array,part_index+1,right)
def partition(array,left,right):
"""Rearrange the array as the number smaller than pivot
is placed on the left and
the number larger than the pivot is placed on the right
the pivot as the split index of array between left and right
Parameters
---------
array : list
A list of numbers
left : int
The index of array
right : int
The index of array
Return
---------
part_index : the index of pivot after rearrangement
"""
# 结束条件
if left >= right :
return
index_left = left # 用于交换,array[left] 是pivot数据
# 使用一个for loop 对subarray数据进行重排。
for i in range(left+1,right+1):
if array[i] <= array[left]: # <= pivot的数据会与大于pivot的数据进行交换。大于pivot的数据储存在大于index_left的右侧
index_left += 1
array[index_left],array[i] = array[i],array[index_left]
array[index_left],array[left] = array[left],array[index_left] # 最后把pivot放在正确的位置,与index_left 交换。
return index_left